|
Analysis of Model-Calculated Soil Moisture over the United States (1931-93) and Application to Long-Range Temperature Forecasts
Jin Huang, Huug van den Dool, and Konstantine P. Georgakakos
-- from "Journal of Climate, Vol.9, No.6, June
1996"
2. The soil moisture model and data
a. Model
Soil moisture
is calculated based on the water balance in the soil. The components of
the water balance in the model are precipitation, evaporation, runoff (or
strearnflow divergence), and groundwater loss. We model the soil moisture
to the extent it participates in landsurface processes, that is, usually
in the upper I - 2 m of soil. The soil moisture budget over an area A can
be expressed as
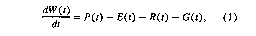
where
W(t) the soil
water content at time t
P(t) the mean
areal precipitation over area A
E(t) the mean
areal evapotranspiration over area A
R(t) the net
strearnflow divergence from area A
G(t) the net
groundwater loss (through deep percolation) from area A.
The strearnflow
divergence R(t) consists of a surface runoff component
S(t) and a subsurface (base flow) runoff component
B(t):
R(t) = S(t) + B(t).
(2)
Following practice
in operational hydrologic forecasting (e.g., Georgakakos 1986), the surface
runoff and the baseflow are parameterized as follows:
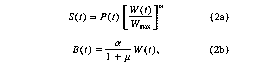
where Wmax
is a measure of the capacity of soils to hold water in millimeters, m is
a parameter with values greater than 1, a is the inverse of the response
time of the baseflow, and y is a dimensionless parameter that determines
the portion of the subsurface flow that becomes baseflow in the channels
draining out from the area of interest. The remaining portion is lost as
unobserved groundwater flow, which is then given as
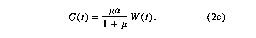
The evapotranspiration
E(t) is estimated in this model as follows:
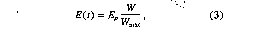
where Ep is
the potential evapotranspiration rate in millimeters per month. The potential
evapotranspiration depends mainly on the net radiative heating on the surface.
However, measurements or sufficiently accurate calculation of the net radiation
on the surface (needed for aerodynamic formulas) are inadequate or absent
over large areas for long times. Term Ep can also
be estimated from pan evaporation, but the observations are lacking and
the estimation has a number of problems (Sellers 1965). In this study,
we calculate the potential evapotranspiration from the observed air temperature
and duration of sunlight using Thornthwaite's method (1948). The rationale
is that air temperature does, to a considerable extent, serve as a parameter
of the net radiation. This is a shortcut of replacing a comprehensive atmospheric
model as well as some interactions by prescribing observed temperature
and precipitation.
Following Thornthwaite
(1948), the formulas of E, are expressed as
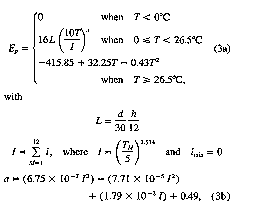
where d is the number of
days in the month, h the number of hours of daylight in the middle day
of the month, and T the monthly mean surface air temperature in
each month of the year.
b. Parameter estimation from
historical data
Parameter estimation
(model calibration) was performed using both manual and automated search-optimization
procedures. The hydrologic literature is replete with methods and applications
of parameterestimation procedures to conceptual hydrologic rainfall-runoff
models (e.g., reviews in Sorooshian 1991; Rajaram and Georgakakos 1989).
Parameter estimation of conceptual models can be thought to be analogous
to experimental calibration of assumed functional relationships in the
laboratory, only with large-scale data from long historical periods. The
data is used to obtain values for the parameters of the functional forms
of the model that represent hydrologic processes, such as surface runoff,
baseflow, etc.
Initial runs
establish an initial set of parameters. The automatic downhill simplex
search method implemented by Press et al. (1989) was used with modifications
pertaining to the establishment of infeasible regions for the parameters.
The automated search procedure estimates parameters based on the changes
in the value of a quantifiable error criterion function for runoff.
The automated
search procedure may converge to local optima or may lock near the boundary
of the feasible region. It is then necessary to start the search from several
initial parameter estimates and select the convergence region with the
lowest criterion value. Once feasible parameter estimates have been obtained
that possess the lowest error, runs of the model are made to examine model
skill in simulating hydrologically important features of the record (i.e.,
magnitude and timing of flood peaks, extended low flow periods, etc.).
Changes in parameter estimates may be necessary to accommodate both a low
error and a good reproduction of the hydrologically important features
of the runoff record. There is considerable judgement involved in the parameter
estimation procedure, which requires hydrologic expertise and familiarity
with model applications.
C. Data and numerical procedure
The atmospheric
datasets used to drive the soil model are monthly surface air temperature
(T) and monthly total precipitation (P) at 344 U.S. climate divisions during
the period 1931-1993. Daily station T and P data at 138 cooperative stations
over 1931-1991 are also used for some specialized questions that require
the use of daily data.
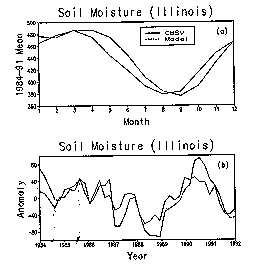
The observed
soil moisture data in Illinois, which is the only available long-term verification
dataset, are used to show the model performance. The observed soil moisture
data are from 16 stations in Illinois for an 8yr period ( 1984 - 1991 )
at 11 layers of soil from the top down to 2 m in the soil (Hollinger and
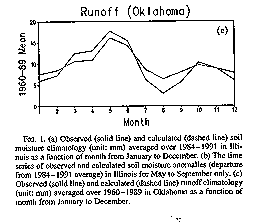
Isard 1994). The observed runoff data (1960-1989) from a 3' by 3' area
in Oklahoma (from 34' to 37'N and 96' to 99'W) are used to calibrate the
model parameters.
The ideal way
to use the model for the entire United States is to estimate the model
parameters for various U.S. regions of similar soil and land cover and
then use these parameters for each region. In this paper, we apply the
parameters estimated in Oklahoma to the entire United States and leave
the model with spatially varying parameters for future work. The model
parameters estimated using the Oklahoma data are Wma~ = 760 mm, p = 5.8,
a = 0.093 mo-', m = 4.886, with the variables E, P, R, and G in units of
millimeters per month. The model integration starts from uniform 200 mm
in January 1931. The spinup time is about 3-4 months.
Because of nonlinear
surface runoff generation, the integration step is varied so as not to
allow the input precipitation to exceed 2 mm per time step. This technique
is also used in the operational NWS Sacramento model (Peck 1974) to prevent
unreasonable runoff. We use the instantaneous' soil moisture estimated
by the model at the end of a month for most of the analyses and to predict
future temperature. However, when comparing with observed soil moisture
(in Fig. 1), we use monthly mean soil moisture. |